Тест 1.16 Защемленная по концам балка, нагруженная равномерно-распределенной нагрузкой

Верификационные тесты ЛИРА-САПР / Тест 1.16 Защемленная по концам балка, нагруженная равномерно-распределенной нагрузкой / Писаренко Г.С., Яковлев А.П., Матвеев В.В. Справочник по сопротивлению материалов. — Киев: Наук. думка, 1988.

Линейные статические задачи для стержневых систем, пластин и оболочек, трехмерные задачи

Аналитическое решение: Писаренко Г.С., Яковлев А.П., Матвеев В.В. Справочник по сопротивлению материалов. — Киев: Наук. думка, 1988.

Формулировка задачи: Защемленная по концам балка нагружается равномерно распределенной нагрузкой q. Определим максимальные поперечное перемещение w.

Исходные данные:

E = 3.0·10⁷Па	- модуль упругости,
μ = 0.25	- коэффициент Пуассона,
l = 2.4 м	- длина балки;
b = 0.2 м	- ширина сечения балки;
h = 0.3 м	- высота сечения балки;
q=10 кН/м	- значение нагрузки.

Результаты расчёта:

При аналитическом решении прогиб в центре балки может быть вычислен по следующей формуле (Писаренко Г.С., Яковлев А.П., Матвеев В.В. Справочник по сопротивлению материалов. — Киев: Наук. думка, 1988).

Примечание: стержневая модель КЭ 10 - универсальный пространственный стержневой КЭ (без учета деформаций поперечного сдвига (рис.1, таб.1), и с учетом сдвига (рис.2)); модель из пластин: КЭ 21 - прямоугольные КЭ плоской задачи (балка-стенка) (рис.1, таб.2); КЭ 28 - прямоугольные КЭ плоской задачи (балка-стенка) с промежуточными узлами на сторонах (рис.2)

РЕЗУЛЬТАТЫ РАСЧЕТА:

Таблица 1

Искомая величина	Аналитическое решение	Результаты расчета (ЛИРА-САПР КЭ 10)	Погрешность,%
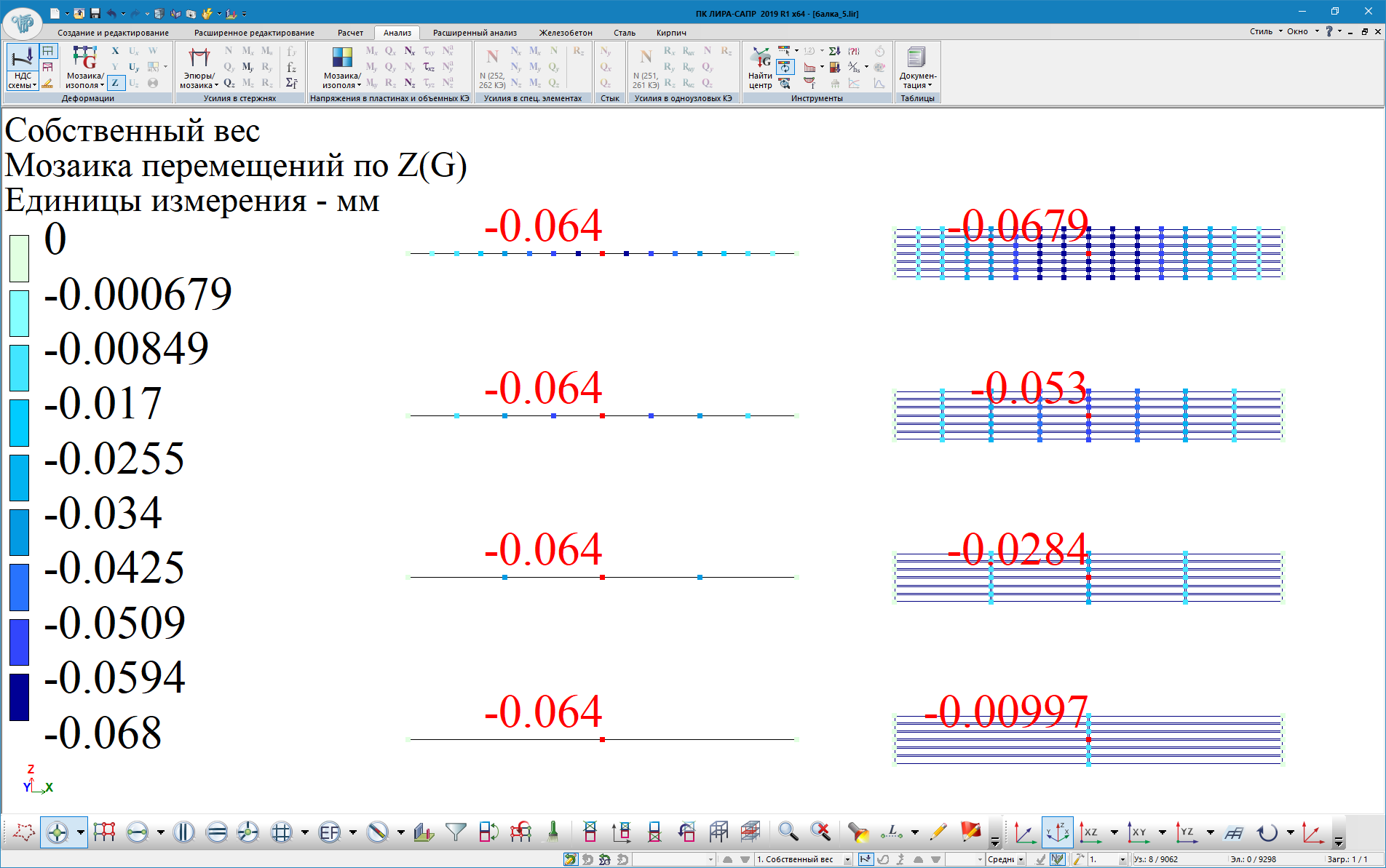
Поперечное перемещение в середине пролета балки, мм	-0.064	-0.064	0.00

Таблица 2

Искомая величина	КЭ сетка с размерностями	Аналитическое решение	Результаты расчета (ЛИРА-САПР КЭ 21)	Погрешность,%
Поперечное перемещение в середине пролета балки, мм	2х6	-0.064	-0.0099	84.53
	4х6		-0.0284	55.62
	8х6		-0.0530	17.19
	16х6		-0.0679	6.09

Рис. 1. Перемещение z, мм в центре балки (без учета деформаций поперечного сдвига)

Рис. 2. Перемещение z, мм в центре балки (c учета деформаций поперечного сдвига)

Примечание: стержневая модель КЭ 10 - универсальный пространственный стержневой КЭ (без учета деформаций поперечного сдвига (рис.1, таб.1), и с учетом сдвига (рис.2)); модель из пластин: КЭ 21 - прямоугольные КЭ плоской задачи (балка-стенка) (рис.1, таб.2); КЭ 28 - прямоугольные КЭ плоской задачи (балка-стенка) с промежуточными узлами на сторонах (рис.2)

Р¤Р°Р№Р»С‹

Текстовый файл исходных данных:
скачать

Возврат к списку

Коментарі

Написати

Верификационные примеры

Тест 1.16 Защемленная по концам балка, нагруженная равномерно-распределенной нагрузкой

Коментарі

Підписатися на розсилку

Слідкуйте за нами