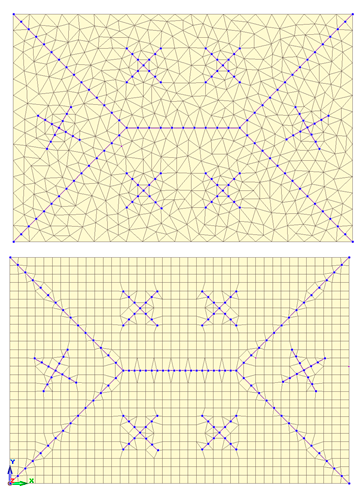
Триангуляція. Побудова скінченних елементів сіток
Побудова скінченно елементних сіток є важливим етапом вирішення задачі по визначенню НДС конструкцій. Цей етап пов'язаний з задоволенням низки суперечливих вимог.
LIRA-FEM* ідеально підходить для розрахунку по методу скінченних елементів. В програмі представлена велика бібліотека скінченних елементів.
LIRA-FEM (ЛІРА-САПР) це програма для розрахунку конструкцій по методу скінченних елементів (МСЕ). У програмному комплексі LIRA-FEM метод скінченних елементів реалізований у формі переміщень – МСЕ розглядається для випадків, коли шуканою вирішальною функцією служить переміщення. Це викликано тим, що вибір розрахункової схеми для МСЕ в переміщеннях легко піддається алгоритмізації, а практичне використання МСЕ неможливе без застосування сучасних комп'ютерів.
Метод скінченних елементів заснований на уявленні суцільного тіла у вигляді сукупності окремих скінченних елементів, що взаємодіють між собою в кінцевому числі точок, які в МСЕ прийнято називати вузлами.
Розрахунок будівельних конструкцій з використанням методу скінченних елементів (МСЕ) є представлення пружних систем у вигляді набору елементів з кінцевим числом ступенів свободи, які з'єднуються між собою у вузлових точках (вузлах). Таке представлення заданої системи призводить до повної формалізації всіх етапів розрахунку. Підхід до розв'язання задачі є єдиним як для стержневих систем, так і для пластин, оболонок, об'ємних тіл і т.п.
Бібліотека скінченних елементів (БСЕ) містить елементи, що моделюють роботу різних типів конструкцій: елементи стержнів, чотирикутні та трикутні елементи плоскої задачі, плити, оболонки, елементи просторової задачі – тетраедр, паралелепіпед, тригранна призма. Крім того, у БСЕ є різні спеціальні елементи, що моделюють в'язь скінченної жорсткості, пружну податливість між вузлами, елементи, що задаються чисельною матрицею жорсткості.
У дужках вказано ознака схеми, де допускається використання СЕ даного типу.
Тип 1. Стержневий СЕ плоскої ферми (1,2,5)
Тип 2. Стержневий СЕ плоскої рами (2,5)
Тип 3. Стержневий СЕ балочного ростверку (3,5)
Тип 4. Стержневий СЕ просторової ферми (4,5)
Тип 7. Просторовий стержневий тонкостінний СЕ з урахуванням депланації перерізу (6)
Тип 10. Універсальний просторовий стержневий КЕ (1,2,3,4,5,6)
Тип 11. Прямокутний СЕ плити (3,5)
Тип 12. Трикутний СЕ плити (3,5)
Тип 15. Універсальний прямокутний СЕ товстої плити (3,5)
Тип 16. Універсальний трикутний СЕ товстої плити (3,5)
Тип 17. Універсальний чотирикутний СЕ товстої плити (3,5)
Тип 19. Чотирикутний СЕ плити (3,5)
Тип 21. Прямокутний СЕ плоскої задачі (балка-стінка) (1,2,5)
Тип 22. Трикутний СЕ плоскої задачі (балка-стінка) (1,2,5)
Тип 23. Універсальний прямокутний СЕ плоскої задачі (балка-стінка) (4,5)
Тип 24. Універсальний трикутний СЕ плоскої задачі (балка-стінка) (4,5)
Тип 27. Універсальний чотирикутний СЕ плоскої задачі (балка-стінка) (4,5)
Тип 30. Чотирикутний СЕ плоскої задачі (балка-стінка) (1,2,5)
Тип 31. Паралелепіпед (4,5)
Тип 32. Тетраедр (4,5)
Тип 33. Пряма трикутна призма (4,5)
Тип 34. Просторовий шестивузловий ізопараметричний КЕ (4,5)
Тип 36. Просторовий восьмивузловий ізопараметричний КЕ (4,5)
Тип 41. Універсальний прямокутний СЕ оболонки (5)
Тип 42. Універсальний трикутний СЕ оболонки (5)
Тип 44. Універсальний чотирикутний СЕ оболонки (5)
Тип 45. Універсальний прямокутний СЕ товстої оболонки (5)
Тип 46. Універсальний трикутний СЕ товстої оболонки (5)/p>
Тип 47. Універсальний чотирикутний СЕ товстої оболонки (5)
Тип 51. Одновузловий СЕ пружної в'язі (1,2,3,4,5)
Тип 52. КЕ задається чисельною матрицею жорсткості. Скінченний елемент, що задається чисельною матрицею жорсткості. Застосовується для налагодження нових типів скінченних елементів.
Тип 53. Законтурний двовузловий СЕ пружної основи (3,4,5)
Тип 54. Законтурний одновузловий СЕ пружної основи (3,4,5)
Тип 55. Двовузловий СЕ пружних в'язів між вузлами (1,2,3,4,5)
Тип 56. Одновузловий СЕ пружних в'язів (1,2,3,4,5)
Тип 57. Одновузловий СЕ одиночної палі (1,2,3,4,5)
Тип 58. Трикутний СЕ стику (5)
Тип 59. Чотирикутний СЕ стику (5)
Тип 60. Двовузловий СЕ багатошарової пружної основи (1,2,3,4,5)
Тип 62. Двовузловий СЕ в'язкого демпфування (1,2,3,4,5)
Тип 67. Двовузловий СЕ для моделювання плоского безмежного ґрунтового масиву (1,2,3,4,5)
Тип 68. Трикутний СЕ для моделювання просторового безмежного ґрунтового масиву (4,5)
Тип 69. Чотирикутний СЕ для моделювання просторового безмежного ґрунтового масиву (4,5)
Тип 82. Трикутний СЕ плоскої задачі (масив) (1,2,5)
Тип 84. Чотирикутний СЕ плоскої задачі (масив) (1,2,5)
Тип 201. Фізично нелінійний стержневий СЕ плоскої ферми (1,2,5)
Тип 202. Фізично нелінійний стержневий СЕ плоскої рами (2,5)
Тип 204. Фізично нелінійний стержневий СЕ просторової ферми (4,5)
Тип 207. Фізично нелінійний двовузловий СЕ попереднього обтиснення (домкрат) (1,2,4,5)
Тип 208. Фізично нелінійний двовузловий СЕ попереднього натягу (1,2,4,5)
Тип 210. Фізично нелінійний універсальний просторовий стержневий КЕ (1,2,3,4,5)
Тип 221. Фізично нелінійний прямокутний СЕ плоскої задачі (балка-стінка) (1,2,5)
Тип 222. Фізично нелінійний трикутний СЕ плоскої задачі (балка-стінка) (1,2,5)
Тип 223. Фізично нелінійний універсальний прямокутний СЕ плоскої задачі (балка-стінка) (4,5)
Тип 224. Фізично нелінійний універсальний трикутний СЕ плоскої задачі (балка-стінка) (4,5)
Тип 227. Фізично нелінійний універсальний чотирикутний СЕ плоскої задачі (балка-стінка) (4,5)
Тип 230. Фізично нелінійний чотирикутний СЕ плоскої задачі (балка-стінка) (1,2,5)
Тип 231. Фізично нелінійний паралелепіпед (4,5)
Тип 232. Фізично нелінійний тетраедр (4,5)
Тип 233. Фізично нелінійна пряма трикутна призма (4,5)
Тип 234. Фізично нелінійний просторовий шестивузловий ізопараметричний КЕ (4,5)
Тип 236. Фізично нелінійний просторовий восьмивузловий ізопараметричний КЕ (4,5)
Тип 241. Фізично нелінійний універсальний прямокутний СЕ оболонки (5)
Тип 242. Фізично нелінійний універсальний трикутний СЕ оболонки (5)
Тип 244. Фізично нелінійний універсальний чотирикутний СЕ оболонки (5)
Тип 245. Фізично нелінійний прямокутний СЕ товстої оболонки (5)
Тип 246. Фізично нелінійний трикутний СЕ товстої оболонки (5)
Тип 247. Фізично нелінійний чотирикутний СЕ товстої оболонки (5)
Тип 251. Одновузловий СЕ односторонньої в'язі з урахуванням граничного зусилля (односторонній аналог СЕ 51 з урахуванням граничного зусилля) (1,2,3,4,5)
Тип 252. Двовузловий СЕ односторонньої в'язі з урахуванням граничного зусилля (1,2,3,4,5)
Тип 255. Двовузловий СЕ пружних в'язів з урахуванням граничних зусиль (аналог СЕ 55 з урахуванням граничних зусиль) (1,2,4,5)
Тип 256. Одновузловий СЕ пружних в'язів з урахуванням граничних зусиль (аналог СЕ 56 з урахуванням граничних зусиль) (1,2,3,4,5)
Тип 258. Трикутний СЕ стику з урахуванням нелінійної роботи (аналог СЕ 58 з урахуванням нелінійної роботи) (5)
Тип 259. Чотирикутний СЕ стику з урахуванням нелінійної роботи (аналог СЕ 59 з урахуванням нелінійної роботи) (5)
Тип 261. Одновузловий СЕ односторонньої пружної в'язі (1,2,3,4,5)
Тип 262. Двовузловий СЕ односторонньої пружної в'язі між вузлами (1,2,3,4,5)
Тип 263. Одновузловий СЕ односторонньої пружної в'язі з тертям (1,2,4,5)
Тип 264. Двовузловий СЕ односторонньої пружної в'язі з тертям між вузлами (1,2,4,5)
Тип 265. Двовузловий СЕ односторонніх пружних в'язів (аналог СЕ 55 з урахуванням односторонньої роботи) (1,2,4,5)
Тип 266. Одновузловий СЕ односторонніх пружних в'язів (аналог СЕ 56 з урахуванням односторонньої роботи) (1,2,3,4,5)
Тип 271. Фізично нелінійний паралелепіпед (ґрунт) (4,5)
Тип 272. Фізично нелінійний тетраедр (ґрунт) (4,5)
Тип 273. Фізично нелінійна пряма трикутна призма (ґрунт) (4,5)
Тип 274. Фізично нелінійний просторовий шестивузловий ізопараметричний СЕ (ґрунт) (4,5)
Тип 276. Фізично нелінійний просторовий восьмивузловий ізопараметричний СЕ (ґрунт) (4,5)
Тип 281. Фізично нелінійний прямокутний СЕ плоскої задачі (ґрунт) (1,2,5)
Тип 282. Фізично нелінійний трикутний СЕ плоскої задачі (ґрунт) (1,2,5)
Тип 284. Фізично нелінійний чотирикутний СЕ плоскої задачі (ґрунт) (1,2,5)
Тип 295. Двовузловий СЕ нелінійних пружних в'язів (аналог СЕ 255 з урахуванням нелінійної роботи) (1,2,4,5)
Тип 296. Одновузловий СЕ нелінійних пружних в'язів (аналог СЕ 256 з урахуванням нелінійної роботи) (1,2,3,4,5)
Тип 308. Геометрично нелінійний двовузловий СЕ для моделювання попереднього натягу (1,2,4,5)
Тип 309. Геометрично нелінійний універсальний просторовий стержневий КЕ, що сильно згинається (1,2,3,4,5)
Тип 310. Геометрично нелінійний універсальний просторовий стержневий СЕ (нитка) (1,2,3,4,5)
Тип 341. Геометрично нелінійний прямокутний СЕ оболонки (5)
Тип 342. Геометрично нелінійний трикутний СЕ оболонки (5)
Тип 344. Геометрично нелінійний чотирикутний СЕ оболонки (5)
Тип 410. Універсальний просторовий стержневий СЕ з урахуванням фізичної та геометричної нелінійності (1,2,3,4,5)
Тип 441. Прямокутний СЕ оболонки з урахуванням фізичної та геометричної нелінійності (5)
Тип 442. Трикутний СЕ оболонки з урахуванням фізичної та геометричної нелінійності (5)
Тип 444. Чотирикутний СЕ оболонки з урахуванням фізичної та геометричної нелінійності (5)
Тип 1505. Стержневий СЕ теплопровідності (15)
Тип 1508. Трикутний СЕ теплопровідності (15)
Тип 1509. Чотирикутний СЕ теплопровідності (15)
Тип 1512. КЕ теплопровідності у формі тетраедру (15)
Тип 1514. Об'ємний шестивузловий СЕ теплопровідності (15)
Тип 1516. Об'ємний восьмивузловий СЕ теплопровідності (15)
Тип 1551. Одновузловий СЕ конвективного теплообміну (15)
Тип 1555. Двовузловий СЕ конвективного теплообміну (15)
Тип 1558. Трикутний СЕ конвективного теплообміну (15)
Тип 1559. Чотирикутний СЕ конвективного теплообміну (15)

Якщо у вас все ще є сумніви, завантажте демонстраційну версію та спробуйте або зв'яжіться з нашою службою підтримки для отримання більш детальної інформації.